Strategy Evaluation, Part 3 - Monte Carlo Simulation
A reality check we all need
Before we dive into Monte Carlo simulation, let's remind ourselves of the basic question we want to answer:
Is a trading strategy any good?
This sounds like it should be a yes or no question, right? Some folks might try to sell you a simple answer, maybe show you a single number or a back test to prove a strategy is worth your money. As we've seen, that's misleading. A simple back test isn't enough. We need to add a bit more nuance to our question.
It's all about the odds
Let's tweak our question and think about it in a slightly different way:
How likely is it that a trading strategy will be any good?
Notice the shift here – we're now thinking about uncertainty, about the chance that our trading strategy might lose money. This is key because every trading strategy is imperfect. Every trading strategy can lose money. Even the strategies designed by the smartest folks out there can hit a rough patch. (You only have to look at the track record of many quantitative funds to see this!)
This is not a bad thing. It's just how it is. To really get the full picture, we need to embrace this uncertainty and think about how we can use it.
We can think about probability with a simple, toy example. Think about flipping a coin. If you bet $10 on heads every flip, you've got a 50% shot at winning. If your odds are just slightly better than 50%, you're set to make money over time. Even 50.01% win rate means you will make money on average.
This basic principle applies to trading, too – if you have better chances than a coin toss, you have an edge. Even 0.01% is an edge.
So our question about likelihood is crucial to strategy evaluation. This explanation is simplified, but I like to start with remembering the basics.
Monte Carlo Simulation: The Casino and the Trader
With that foundation, let's talk about Monte Carlo simulation. At its heart, this tool helps us quantify uncertainty. "Quantify uncertainty" sounds impossible, and truly, many, many researchers more brilliant than me spend countless hours pioneering progress on the topic. And this tool, though imperfect, gives us great insights into the chance our strategy works.
Here's the setup. We've backtested and optimized a strategy and have the parameters we want to take to live trading. We know the past, but we don't know the future. This is exactly the same concept of an in-sample and out-of-sample split, shown here:
We hypothetically stand at the end of the purple line at the beginning of 2021, and we don't know about the gold line yet. At that point in time, the price could go in a lot of directions.
Monte Carlo simulation asks "What if?" a huge number of times. What if the price went in a certain direction? What would happen? We make certain assumptions about the price’s movement, and we simulate random scenarios then evaluate our strategy on each scenario.
Keeping it Real With a P-value
This approach gives us what amounts to a reality check, as Halbert White famously put it. Because reality is inherently uncertain. It's like we're putting our strategy through a reality TV show challenge to see if it's really as good as it thinks it is. By running a bunch of simulations, we can see if our strategy's results are actually impressive or just average.
We sum this assessment up with a p-value. To get to a p-value, we calculate our strategy's performance under each hypothetical scenario and compare with the performance using the original price series.
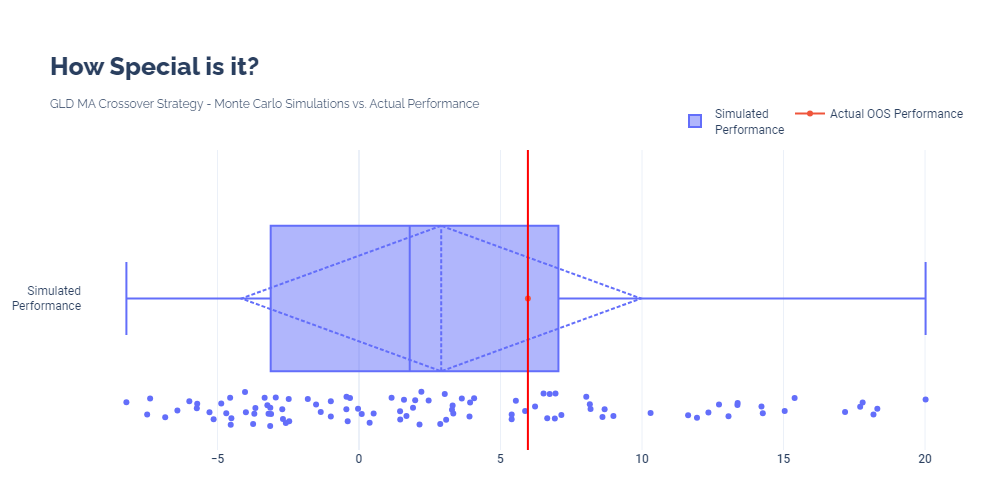
In this example, we continue using our MA crossover strategy with GLD. For this IS/OOS split, we calculate the strategy's OOS annualized return for each scenario using the optimal strategy parameters from the IS backtest. This visual shows that our return is better than about 70% of the simulations. Our p-value is the number of times a simulation performed better divided by the total number of simulations - 0.3.
Far more talented researchers have developed more sophisticated approaches to Monte Carlo simulation, but I like this approach because it is intuitive and easy to interpret. (We might alter our approach in the future - your thoughts are welcome)
How to Interpret a P-value
If you're like me, high school statistics is just a fuzzy memory by now. The phrase "statistical significance" comes to mind, but really, most days I have so many significant things to think about.
At the risk of angering our statistician friends, I like to think of statistical significance as "being special." We are trying to measure measure how "special" our result is.
But if our strategy is profitable, does it matter how special it is? The money in our bank account doesn't care about the p-value. A profitable strategy is a profitable strategy.
Imagine you are racing a horse in the Kentucky Derby and a car in the Indy 500. Say both your horse and your car win their races. That's great, and we'd all be excited about it. But what if your horse was faster than 95% of other winners (p-value: 0.05), while your car was faster than only 60% of other winners (p-value: 0.4)? Suddenly, that horse looks much more interesting.
A p-value captures that in a single number. Our horse is much more "special" than our car, even though the car is faster than the horse and won its race, too.
We do not want to ignore the nuances here, however. Being "special" can mean very different things. It could mean that we have a legitimately good trading strategy. It could also mean that we have a fluke, like a single trade that was wildly profitable and makes up most of our profits.
In other words, statistical significance includes extremely unlikely black swan events, too. We want to think carefully about gambling on long-tail events.
Being "not special" can mean very different things, as well. A high p-value from a Monte Carlo simulation does say that our strategy performs about as well or worse than random simulations, which does not speak highly of it. But if a profitable strategy has a high p-value, we could also say that the result might be more typical and "safer".
We don't want to say that this discussion covers everything about statistical significance. We have glossed over many properties of p-values and simplified their interpretation, and we have completely ignored other statistical tests used in practice. If you are interested in learning more, statistical significance truly is a rich field of study. Our goal here is to share the intuition behind how we think about p-values in our tests and what information we try to communicate.
Putting it all Together
Monte Carlo simulation helps keep us grounded. It's a reminder that we're always dealing with uncertainty in trading. And while we might love our strategies, it's crucial to keep testing them against what could happen. That way, we're not just hoping for the best – we're planning for it, with a good understanding of the risks and rewards.
So, when you're looking at a trading strategy, it's not just about whether it makes money. It's about understanding how likely it is to continue doing so, considering all the different ways the market could move. That's what helps us decide if a strategy is any good.
Until next time, keep on the cutting edge, friends.
References
White, H. (2000). A Reality Check for Data Snooping. Econometrica, 68(5), 1097–1126. http://www.jstor.org/stable/2999444
Disclaimers
The content on this page is for educational and informational purposes only. Any views and opinions expressed belong only to the writer and do not represent views and opinions of people, institutions, or organizations that the writer may or may not be associated with.
No material in this page should be construed as buy/sell recommendations, investment advice, determinations of suitability, or solicitations. Securities investment and trading involve risks, and not all risks are disclosed or discussed here. Loss of principal is possible. You are encouraged to seek financial advice from a licensed professional prior to making transaction decisions.
Further, you should not assume that the future performance of any specific investment or investment strategy will be profitable or equal to corresponding past performance levels. Past performance does not guarantee future results.